-
[알고리즘] 동적 계획법 (Dynamic Programming)Algorithm 2024. 1. 6. 12:06728x90
동적 계획법이란?
하나의 큰 문제를 여러개의 작은 단위의 문제로 나누고 작은 단위의 문제를 먼저 해결 후 결과를 저장한 뒤 더 큰 단위의 문제를 해결할 때 재활용하여 사용됩니다.
동적 계획법은 재귀 함수와 동작 방식이 유사합니다. 하지만 재귀 함수는 작은 단위의 문제 해결이 여러번 반복 될 수 있는 구조입니다. 대표적인 예시인 피보나치 수열로 보면 점화식은
f(n) = f(n - 1) + f(n-2)이지만 f(n - 1), f(n-2)에서 각 함수를 한번씩 더 호출하면 동일한 값을 2번씩 구하게 되고 그로인해 피보나치 수를 구하기 위한 함수의 호출 횟수는 기하급수 적으로 증가하게 되고 시간 복잡도는O(n^2)가 됩니다.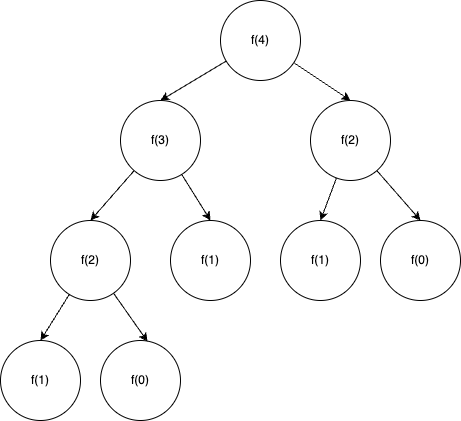
동적 계획법을 사용하게 된다면 작은 단위의 문제를 저장하게 되어 중복된 계산을 방지할 수 있고 시간복잡도는
O(n)으로 해결할 수 있습니다.조건
- 작은 문제에서 반복이 발생
- 같은 문제는 항상 정답이 같음
위 두 조건이 만족된다면 메모이제이션을 통해 큰 문제를 해결 가능합니다.
구현 방법
Top Down
private static int[] memoization; public static int getFibonacci(int n) { memoization = new int[n]; memoization[0] = 1; memoization[1] = 1; return dp(n); } private static int dp(int n) { if (memoization[n] != 0) { return memoization[n]; } memoization[n] = dp(n - 1) + dp(n - 2); return memoization[n]; }Bottom Up
private static int[] memoization; public static int getFibonacci(int n) { memoization = new int[n]; memoization[0] = 1; memoization[1] = 1; for (var i = 2; i < n; i++) { memoization[i] = memoization[i - 1] + memoization[i - 2]; } return memoization[n - 1]; }728x90'Algorithm' 카테고리의 다른 글
[Algorithm] 이진 탐색(Binary search) (0) 2023.12.28 [알고리즘] 누적합 알고리즘 (0) 2023.12.25 [Programmers] 거리두기 확인하기 JAVA (0) 2023.12.17 [Programmers] 숫자 변환하기 (Java) (0) 2023.09.06 [Programmers] 무인도 여행 (JAVA) (0) 2023.09.03